Расчет размерных цепей
Обратная задача
Пример решения обратной задачи методом максимума-минимума.
Расчет размерных цепей онлайн. Обратная задача.
Задание:
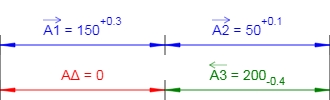
Рассчитать заданную размерную цепь (см. рис. 1) по методу максимума-минимума (max/min).
Исходные данные:
A1 = 150+0,3 (мм);
A2 = 50+0,1 (мм);
A3 = 200-0,4 (мм);
Увеличивающие звенья: A1, A2;
Уменьшающие звенья: A3;
Замыкающее звено: AΔ
Решение:
1. Определение характеристик составляющих звеньев размерной цепи.
1.1. Расчет предельных размеров звеньев размерной цепи.
Наибольший размер i-го звена определяется по формуле:
A1 max = 150 + 0,3 = 150,3(мм)
A2 max = 50 + 0,1 = 50,1(мм)
A3 max = 200 + 0 = 200(мм)
Наименьший размер i-го звена определяется по формуле:
A1 min = 150 + 0 = 150(мм)
A2 min = 50 + 0 = 50(мм)
A3 min = 200 + (-0,4) = 199,6(мм)
1.2. Расчет допусков звеньев размерной цепи.
Допуск i-го звена размерной цепи определим по формуле:
T(A1) = 0,3 - 0 = 0,3(мм)
T(A2) = 0,1 - 0 = 0,1(мм)
T(A3) = 0 - (-0,4) = 0,4(мм)
1.3. Расчет координаты середины поля допуска звеньев размерной цепи.
Середину поля допуска i-го звена определим по формуле:
тогда
2. Определение характеристик замыкающего звена.
2.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:
Тогда для заданной размерной цепи формула (5) принимает вид:
AΔ = A1 + A2 - A3
AΔ = 150 + 50 - 200 = 0(мм)
2.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:
Тогда для заданной размерной цепи формула (6) принимает вид:
T(AΔ) = T(A1) + T(A2) + T(A3)
T(AΔ) = 0,3 + 0,1 + 0,4 = 0,8(мм)
2.3.Координата середины поля допуска замыкающего звена определяется по формуле:
Координата середины поля допуска замыкающего звена определяется по формуле:
C(AΔ) = A1 + A2 - A3
C(AΔ) = 0,15 + 0,05 - (-0,2) = 0,4(мм)
2.3.1 Предельные отклонения замыкающего звена
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
Тогда:
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
Тогда:
2.4. Максимальные и минимальные значения зазоров и натягов:
Максимальный зазор определяется по формуле:
Для заданной размерной цепи формула (10) принимает вид:
S max = A1 max + A2 max - A3 min
S max = 150,3 + 50,1 - 199,6 = 0,8
Минимальный зазор определяется по формуле:
Для заданной размерной цепи формула (11) принимает вид:
S min = A1 min + A2 min - A3 max
S min = 150 + 50 - 200 = 0
Для сборочной размерной цепи:
В замыкающем звене образуется зазор:
S max = 0,8
S min = 0
3. Результаты расчета
Замыкающее звено:
AΔ = 0+0,8 (мм);
Для сборочной размерной цепи:
В замыкающем звене образуется зазор:
S max = 0,8
S min = 0
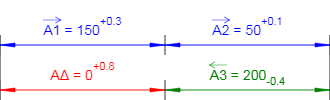
Рисунок 2 - Схема размерной цепи. Результаты расчета.
Рассчитать заданную размерную цепь (см. рис. 1) по методу максимума-минимума (max/min).
Исходные данные:

Рисунок 1 - Схема размерной цепи. Исходные данные.
Звенья размерной цепи:A1 = 150+0,3 (мм);
A2 = 50+0,1 (мм);
A3 = 200-0,4 (мм);
Увеличивающие звенья: A1, A2;
Уменьшающие звенья: A3;
Замыкающее звено: AΔ
Решение:
1. Определение характеристик составляющих звеньев размерной цепи.
1.1. Расчет предельных размеров звеньев размерной цепи.
Наибольший размер i-го звена определяется по формуле:
| Ai max = Ai + Es(Ai) | (1) |
где
A i – номинальное значение i-го звена;
Es(A i ) – верхнее отклонение звена;
i – индекс звена;
A i – номинальное значение i-го звена;
Es(A i ) – верхнее отклонение звена;
i – индекс звена;
A1 max = 150 + 0,3 = 150,3(мм)
A2 max = 50 + 0,1 = 50,1(мм)
A3 max = 200 + 0 = 200(мм)
Наименьший размер i-го звена определяется по формуле:
| Ai min = Ai + Ei(Ai) | (2) |
где
Ei(A i ) – нижнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
A1 min = 150 + 0 = 150(мм)
A2 min = 50 + 0 = 50(мм)
A3 min = 200 + (-0,4) = 199,6(мм)
1.2. Расчет допусков звеньев размерной цепи.
Допуск i-го звена размерной цепи определим по формуле:
| T(A i ) = Es(A i ) - Ei(A i ) | (3) |
T(A1) = 0,3 - 0 = 0,3(мм)
T(A2) = 0,1 - 0 = 0,1(мм)
T(A3) = 0 - (-0,4) = 0,4(мм)
1.3. Расчет координаты середины поля допуска звеньев размерной цепи.
Середину поля допуска i-го звена определим по формуле:
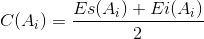 | (4) |
тогда
| C(A1) = | (0,3 + 0) | = 0,15 (мм); |
| 2 |
| C(A2) = | (0,1 + 0) | = 0,05 (мм); |
| 2 |
| C(A3) = | (0 + (-0,4)) | = -0,2 (мм); |
| 2 |
2. Определение характеристик замыкающего звена.
2.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:
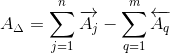 | (5) |
где
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
Тогда для заданной размерной цепи формула (5) принимает вид:
AΔ = A1 + A2 - A3
AΔ = 150 + 50 - 200 = 0(мм)
2.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:
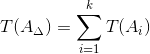 | (6) |
где
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
Тогда для заданной размерной цепи формула (6) принимает вид:
T(AΔ) = T(A1) + T(A2) + T(A3)
T(AΔ) = 0,3 + 0,1 + 0,4 = 0,8(мм)
2.3.Координата середины поля допуска замыкающего звена определяется по формуле:
Координата середины поля допуска замыкающего звена определяется по формуле:
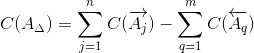 | (7) |
где
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
C(AΔ) = A1 + A2 - A3
C(AΔ) = 0,15 + 0,05 - (-0,2) = 0,4(мм)
2.3.1 Предельные отклонения замыкающего звена
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
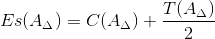 | (8) |
где
C(A Δ) - координата середины поля допуска замыкающего звена
T(A Δ) - допуск замыкающего звена;
C(A Δ) - координата середины поля допуска замыкающего звена
T(A Δ) - допуск замыкающего звена;
Тогда:
| Es(AΔ) = 0,4 + | 0,8 | = 0,8 (мм); |
| 2 |
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
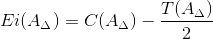 | (9) |
Тогда:
| Ei(AΔ) = 0,4 - | 0,8 | = 0 (мм); |
| 2 |
2.4. Максимальные и минимальные значения зазоров и натягов:
Максимальный зазор определяется по формуле:
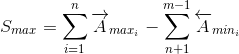 | (10) |
S max = A1 max + A2 max - A3 min
S max = 150,3 + 50,1 - 199,6 = 0,8
Минимальный зазор определяется по формуле:
 | (11) |
S min = A1 min + A2 min - A3 max
S min = 150 + 50 - 200 = 0
Для сборочной размерной цепи:
В замыкающем звене образуется зазор:
S max = 0,8
S min = 0
3. Результаты расчета
Замыкающее звено:
AΔ = 0+0,8 (мм);
Для сборочной размерной цепи:
В замыкающем звене образуется зазор:
S max = 0,8
S min = 0

Рисунок 2 - Схема размерной цепи. Результаты расчета.
Расчет размерных цепей онлайн. Обратная задача.