Расчет размерных цепей
Прямая задача
Пример решения прямой задачи методом полной взаимозаменяемости
Способ равных квалитетов
Расчет размерных цепей онлайн. Прямая задача.
Задание:Рассчитать заданную размерную цепь (см. рис. 1) по методу полной взаимозаменяемости (max/min).
Допуски на составляющие звенья определять способом равных квалитетов (одного квалитета).
Сделать проверку выполненных расчетов.
Исходные данные:
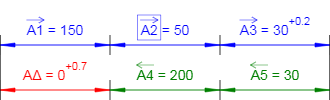
Рисунок 1 - Схема размерной цепи. Исходные данные.
Звенья размерной цепи:
A1 = 150 (мм)
A2 = 50 (мм)
A3 = 30+0,2 (мм) - звено с известным допуском;
A4 = 200 (мм)
A5 = 30 (мм)
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5;
Компенсирующее звено: A2
Замыкающее звено: AΔ
Верхнее отклонение замыкающего звена Es(AΔ) = 0,7 мм
Нижнее отклонение замыкающего звена: Ei(AΔ) = 0 мм
Решение:
1. Определение характеристик замыкающего звена.
1.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:
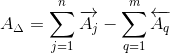 | (1) |
где
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
Тогда для заданной размерной цепи формула (1) принимает вид:
AΔ = A1 + A2 + A3 - (A4 + A5)
AΔ = 150 + 50 + 30 - (200 + 30) = 0(мм)
1.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:
| T(A Δ ) = Es(A Δ ) - Ei(A Δ ) | (2) |
где
Es(A Δ ) – верхнее отклонение замыкающего звена;
Ei(A Δ ) – нижнее отклонение замыкающего звена;
Es(A Δ ) – верхнее отклонение замыкающего звена;
Ei(A Δ ) – нижнее отклонение замыкающего звена;
тогда
T(AΔ) = 0,7 - 0 = 0,7(мм)
2. Определение характеристик составляющих звеньев размерной цепи.
2.1. Определение допусков составляющих звеньев
2.1.1 Определение значений единиц допуска составляющих звеньев.
По таблице 1 принимаем количество единиц допуска для каждого звена.
Таблица 1 - Значение единиц допуска i для различных интервалов размеров.
| Интервалы размеров, мм | 1-3 | 3-6 | 6-10 | 10-18 | 18-30 | 30-50 | 50-80 | 80-120 | 120-180 | 180-250 | 250-315 | 315-400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i, мкм | 0,55 | 0,73 | 0,90 | 1,08 | 1,31 | 1,56 | 1,86 | 2,17 | 2,52 | 2,90 | 3,23 | 3,54 |
A1 = 150, i1 = 2,52;
A2 = 50, i2 = 1,56;
A4 = 200, i4 = 2,89;
A5 = 30, i5 = 1,31;
2.1.2 Определение числа единиц допуска.
Число единиц допуска "а" находим по формуле:
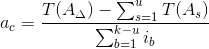 | (3) |
где
T(A Δ) - допуск замыкающего звена;
T(A s ) - допуск звена с известным допуском;
k – число звеньев размерной цепи;
u - число звеньев с известным допуском;
s - индекс звена с известным допуском;
b - индекс звена с неизвестным допуском;
ib - значение единицы допуска, мкм
T(A Δ) - допуск замыкающего звена;
T(A s ) - допуск звена с известным допуском;
k – число звеньев размерной цепи;
u - число звеньев с известным допуском;
s - индекс звена с известным допуском;
b - индекс звена с неизвестным допуском;
ib - значение единицы допуска, мкм
Тогда для заданной размерной цепи формула (3) принимает вид:
| аc = | T(AΔ) - T(A3) | |
| i1 + i2 + i4 + i5 |
| аc = | 700 - 200 | = 60,4 |
| 2,52 + 1,56 + 2,89 + 1,31 |
2.1.3 Определение квалитетов составляющих звеньев.
По числу единиц допуска аc=60,4 принимаем квалитет 9 (см. табл.2).
Таблица 2 - Число единиц допуска, содержащихся в допуске по квалитетам, коэффициент точности «а».
| Квалитет IT | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэф. точн. а | 7 | 10 | 16 | 25 | 40 | 64 | 100 | 160 | 250 | 400 | 640 | 1000 |
На составляющие звенья назначаем допуски по 9 квалитету (см. табл.3).
На увеличивающие размеры допуски назначаем по H
На уменьшающие размеры допуски назначаем по h
A1 = 150H9(+0,1) (мм);
A4 = 200h9(-0,115) (мм);
A5 = 30h9(-0,052) (мм);
Таблица 3 - Величины допусков (мкм) для различных интервалов размеров (мм) и квалитетов
| Квалитеты | Интервалы (свыше) – до, мм | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| До 3 | 3-6 | 6-10 | 10-18 | 18-30 | 30-50 | 50-80 | 80-120 | 120-180 | 180-250 | 250-315 | 315-400 | 400-500 | |
| 5 | 4 | 5 | 6 | 8 | 9 | 11 | 13 | 15 | 18 | 20 | 23 | 25 | 27 |
| 6 | 6 | 8 | 9 | 11 | 13 | 16 | 19 | 22 | 25 | 29 | 32 | 36 | 40 |
| 7 | 10 | 12 | 15 | 18 | 21 | 25 | 30 | 35 | 40 | 46 | 52 | 57 | 63 |
| 8 | 14 | 18 | 22 | 27 | 33 | 39 | 46 | 54 | 63 | 72 | 81 | 89 | 97 |
| 9 | 25 | 30 | 36 | 43 | 52 | 62 | 74 | 87 | 100 | 115 | 130 | 140 | 155 |
| 10 | 40 | 48 | 58 | 70 | 84 | 100 | 120 | 140 | 160 | 185 | 210 | 230 | 250 |
| 11 | 60 | 75 | 90 | 110 | 130 | 160 | 190 | 220 | 250 | 290 | 320 | 360 | 400 |
| 12 | 100 | 120 | 150 | 180 | 210 | 250 | 300 | 350 | 400 | 460 | 520 | 570 | 630 |
| 13 | 140 | 180 | 220 | 270 | 330 | 390 | 460 | 540 | 630 | 720 | 810 | 890 | 970 |
| 14 | 250 | 300 | 360 | 430 | 520 | 620 | 740 | 870 | 1000 | 1150 | 1300 | 1400 | 1550 |
| 15 | 400 | 480 | 580 | 700 | 840 | 1000 | 1200 | 1400 | 1600 | 1850 | 2100 | 2300 | 2500 |
| 16 | 600 | 750 | 900 | 1100 | 1300 | 1600 | 1900 | 2200 | 2500 | 2900 | 3200 | 3600 | 4000 |
2.3. Определение середины поля допуска i-го звена
Середину поля допуска i-го звена определим по формуле:
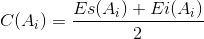 | (4) |
где
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
тогда
| С(A1) = | (0,1 + 0) | = 0,05 |
| 2 |
| С(A3) = | (0,2 + 0) | = 0,1 |
| 2 |
| С(A4) = | (0 + (-0,115)) | = -0,0575 |
| 2 |
| С(A5) = | (0 + (-0,052)) | = -0,026 |
| 2 |
3. Определение характеристик компенсирующего звена.
Компенсирующее звено: A2 - увеличивающее звено
3.1. Определение допуска компенсирующего звена.
Допуск компенсирующего звена определим по формуле:
 | (5) |
где
Т(А i ) – допуск любого составляющего звена;
T(A k) - допуск компенсирующего звена;
Т(А i ) – допуск любого составляющего звена;
T(A k) - допуск компенсирующего звена;
Тогда для заданной размерной цепи формула (5) принимает вид:
T(A2к) = T(AΔ) - (T(A1) + T(A3) + T(A4) + T(A5))
тогда
TA2к = 0,7 - (0,1 + 0,2 + 0,115 + 0,052) = 0,233 (мм)
3.2. Определение середины поля допуска компенсирующего звена
Середину поля допуска компенсирующего звена определим по формуле:
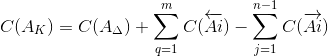 | (6) |
где
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
C(A Δ) - координата середины поля допуска замыкающего звена
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
C(A Δ) - координата середины поля допуска замыкающего звена
Тогда для заданной размерной цепи формула (6) принимает вид:
C(A2к) = C(AΔ) + (C(A4) + C(A5)) - (C(A1) + C(A3))
тогда
С(A2к) = 0,35 + ((-0,0575) + (-0,026)) - (0,05 + 0,1) = 0,1165
3.3. Определение верхнего отклонения компенсирующего звена
Верхнее отклонение компенсирующего звена определим по формуле:
| Es(Ak ) = C(Ak ) + 0,5⋅T(k ) | (7) |
где
C(A k) - координата середины поля допуска компенсирующего звена;
C(A k) - координата середины поля допуска компенсирующего звена;
тогда
Es(Aк) = 0,1165 + (0,5⋅0,233) = 0,233
3.4. Определение нижнего отклонения компенсирующего звена
Нижнее отклонение компенсирующего звена определим по формуле:
| Ei(Ak ) = C(Ak ) - 0,5⋅T(k ) | (8) |
тогда
Ei(Aк) = 0,1165 - (0,5⋅0,233) = 0
Результаты расчета.
Звенья размерной цепи с определенными допусками:
A1 = 150H9(+0,1) (мм);
A2 = 50+0,233 (мм);
A3 = 30+0,2 (мм);
A4 = 200h9(-0,115) (мм);
A5 = 30h9(-0,052) (мм);
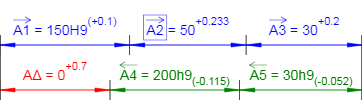
Рисунок 2 - Схема размерной цепи. Результаты расчета.
Проверка расчета.
Проверка правильности решения задачи производится по формулам:
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
 | (9) |
где
Es(A j ) – верхнее отклонение любого увеличивающего звена;
Ei(A q ) – нижнее отклонение любого уменьшающего звена;
Es(A j ) – верхнее отклонение любого увеличивающего звена;
Ei(A q ) – нижнее отклонение любого уменьшающего звена;
Тогда для заданной размерной цепи формула (9) принимает вид:
Es(AΔ) = Es(A1) + Es(A2) + Es(A3) - (Ei(A4) + Ei(A5))
тогда
Es(AΔ) = 0,1 + 0,233 + 0,2 - ((-0,115) + (-0,052)) = 0,7
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
 | (10) |
где
Ei(A i ) – нижнее отклонение любого увеличивающего звена;
Es(A q ) – верхнее отклонение любого уменьшающего звена;
Ei(A i ) – нижнее отклонение любого увеличивающего звена;
Es(A q ) – верхнее отклонение любого уменьшающего звена;
Тогда для заданной размерной цепи формула (10) принимает вид:
Ei(AΔ) = Ei(A1) + Ei(A2) + Ei(A3) - (Es(A4) + Es(A5))
тогда
Ei(AΔ) = 0 + 0 + 0 - (0 + 0) = 0