Расчет размерных цепей
Обратная задача
теоретико-вероятностный метод
Теоретико-вероятностный метод - метод расчета, учитывающий рассеяние размеров
и вероятность различных сочетаний отклонений составляющих звеньев размерной цепи.
Применение теории вероятностей позволяет расширить допуски составляющих размеров
и тем самым облегчить изготовление деталей при практически ничтожном риске
несоблюдения предельных значений замыкающего размера.
Расчет размерных цепей онлайн. Обратная задача.
Формулы
1. Определение характеристик составляющих звеньев размерной цепи
1.1. Допуск i-го звена размерной цепи определим по формуле:
1.2. Середину поля допуска i-го звена определим по формуле:
2. Определение характеристик замыкающего звена
2.1. Номинальное значение замыкающего звена AΔ определим по формуле:
2.2. Допуск замыкающего звена AΔ определим по формуле:
2.3. Координата середины поля допуска замыкающего звена определяется по формуле:
2.4. Предельные отклонения замыкающего звена.
2.4.1 Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
2.4.2. Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
Пример
Задание:
Требуется проверить наличие и величину зазора AΔ.
Определить допуск и предельные отклонения размера замыкающего звена (см. рис. 1) по теоретико-вероятностному методу, приняв t=3, λ2 = 1/9,
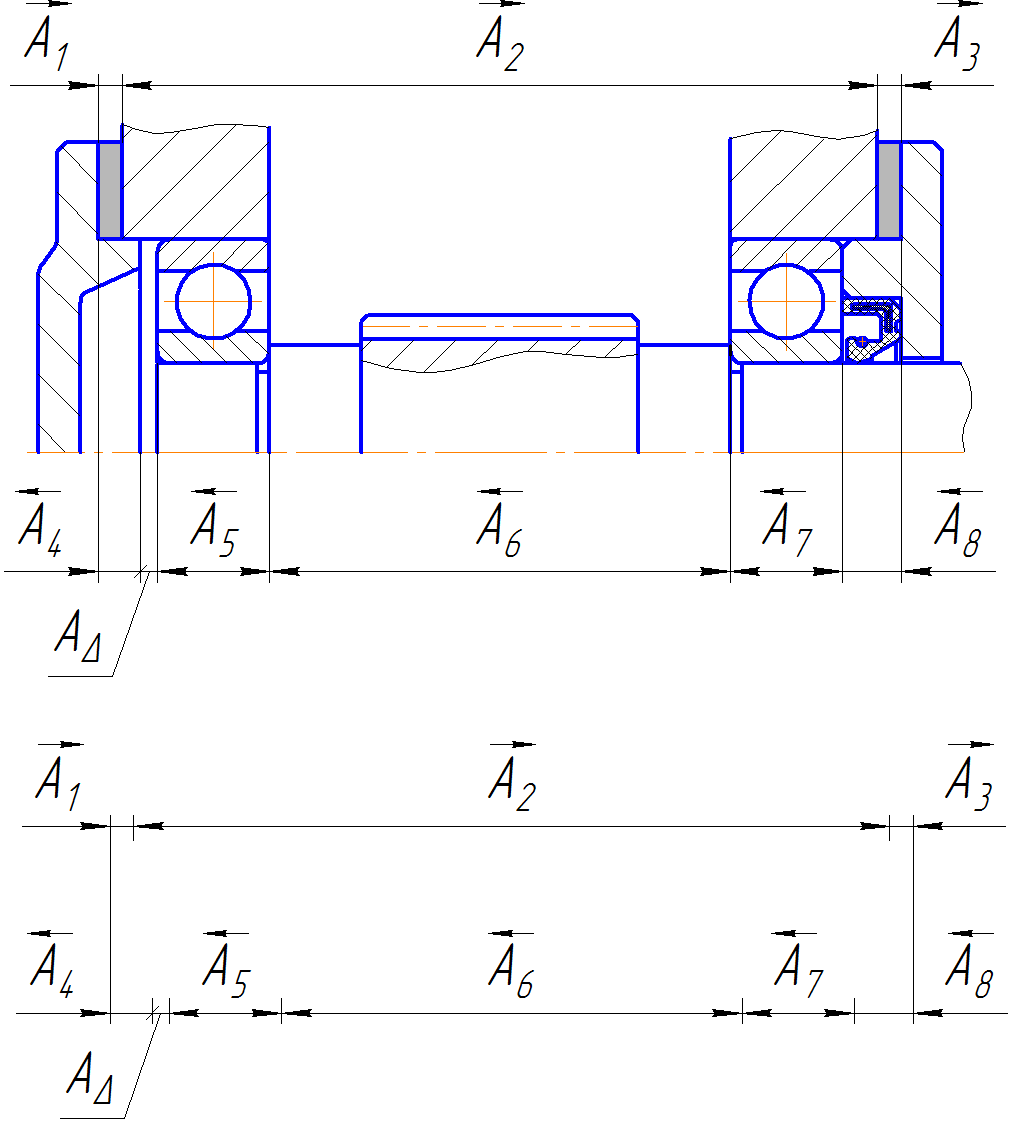
Рисунок 1 – Сборочная размерная цепь.
Исходные данные:
Звенья размерной цепи:
Допуски и координаты середины поля допуска составляющих звеньев определены по формулам (1) и (2).
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5, A6, A7, A8;
Замыкающее звено: AΔ
Решение:
1. Номинальный размер замыкающего звена
Номинальный размер замыкающего звена AΔ определим по формуле
Для заданной размерной цепи формула (3) принимает вид:
AΔ = A1 + A2 + A3 - (A4 + A5 + A6 + A7 + A8)
AΔ = 1 + 206 + 1 - (10 + 19 + 150 + 19 + 10) = 0(мм)
2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле
Для заданной размерной цепи формула (4) принимает вид:
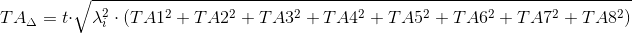
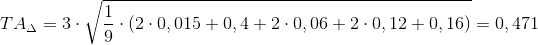
3. Координаты середины поля допуска замыкающего звена
Координату середины поля допуска замыкающего звена определим по формуле
Для заданной размерной цепи формула (5) принимает вид:
С(AΔ) = С(A1) + С(A2) + С(A3) - (С(A4) + С(A5) + С(A6) + С(A7) + С(A8))
С(AΔ) = (-0,0075) + 0,15 + (-0,0075) - ((-0,03) + (-0,06) + (-0,16) + (-0,06) + (-0,03)) = 0,475 (мм)
4. Предельные отклонения замыкающего звена
4.1. Верхнее отклонение замыкающего звена EsAΔ определим по формуле EsAΔ = 0,475 + 0,5·0,471 = 0,71(мм)
4.2. Нижнее отклонение замыкающего звена EiAΔ определим по формуле EiAΔ = 0,475 - 0,5·0,471 = 0,24(мм)
1. Определение характеристик составляющих звеньев размерной цепи
1.1. Допуск i-го звена размерной цепи определим по формуле:
| T(A i ) = Es(A i ) - Ei(A i ) | (1) |
где
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
i – индекс звена;
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
i – индекс звена;
1.2. Середину поля допуска i-го звена определим по формуле:
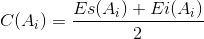 | (2) |
2. Определение характеристик замыкающего звена
2.1. Номинальное значение замыкающего звена AΔ определим по формуле:
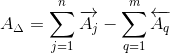 | (3) |
где
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
2.2. Допуск замыкающего звена AΔ определим по формуле:
 | (4) |
где
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
λ - коэффициент относительного рассеяния.
Зависит от принятого закона распределения размера:
— для нормального распределения(Гаусса) λ 2 = 1/9,
— для закона треугольника(Симпсона) λ 2 = 1/6,
— для закона равной вероятности λ 2 = 1/3.
t - коэффициент риска, определяющий количество бракованных деталей;
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
λ - коэффициент относительного рассеяния.
Зависит от принятого закона распределения размера:
— для нормального распределения(Гаусса) λ 2 = 1/9,
— для закона треугольника(Симпсона) λ 2 = 1/6,
— для закона равной вероятности λ 2 = 1/3.
t - коэффициент риска, определяющий количество бракованных деталей;
| p | 32 | 23 | 16 | 9 | 4,6 | 2,1 | 0,94 | 0,51 | 0,27 | 0,1 |
|---|---|---|---|---|---|---|---|---|---|---|
| t | 1 | 1,2 | 1,4 | 1,7 | 2 | 2,3 | 2,6 | 2,8 | 3 | 3,3 |
2.3. Координата середины поля допуска замыкающего звена определяется по формуле:
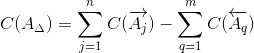 | (5) |
где
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
2.4. Предельные отклонения замыкающего звена.
2.4.1 Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
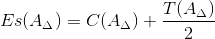 | (6) |
где
C(A Δ) - координата середины поля допуска замыкающего звена
T(A Δ) - допуск замыкающего звена;
C(A Δ) - координата середины поля допуска замыкающего звена
T(A Δ) - допуск замыкающего звена;
2.4.2. Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
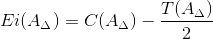 | (7) |
Пример
Задание:
Требуется проверить наличие и величину зазора AΔ.
Определить допуск и предельные отклонения размера замыкающего звена (см. рис. 1) по теоретико-вероятностному методу, приняв t=3, λ2 = 1/9,

Рисунок 1 – Сборочная размерная цепь.
Исходные данные:
Звенья размерной цепи:
Допуски и координаты середины поля допуска составляющих звеньев определены по формулам (1) и (2).
| A1 = 1-0,015 (мм); | Т(A1)=0,015 (мм); | C(A1) = -0,0075 (мм); | ||||
|
Т(A2)=0,4 (мм); | C(A2) = 0,15(мм); | ||||
| A3 = 1-0,015 (мм); | Т(A3)=0,015 (мм); | C(A3) = -0,0075 (мм); | ||||
| A4 = 10-0,06 (мм); | Т(A4)=0,06 (мм); | C(A4) = -0,03 (мм); | ||||
| A5 = 19-0,12 (мм); | Т(A5)=0,12 (мм); | C(A5) = -0,06 (мм); | ||||
|
Т(A6)=0,16 (мм); | C(A6) = -0,16 (мм); | ||||
| A7 = 19-0,12 (мм); | Т(A7)=0,12 (мм); | C(A7)= -0,06 (мм); | ||||
| A8 = 10-0,06 (мм); | Т(A8)=0,06 (мм); | C(A8)= -0,03 (мм); |
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5, A6, A7, A8;
Замыкающее звено: AΔ
Решение:
1. Номинальный размер замыкающего звена
Номинальный размер замыкающего звена AΔ определим по формуле
Для заданной размерной цепи формула (3) принимает вид:
AΔ = A1 + A2 + A3 - (A4 + A5 + A6 + A7 + A8)
AΔ = 1 + 206 + 1 - (10 + 19 + 150 + 19 + 10) = 0(мм)
2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле
Для заданной размерной цепи формула (4) принимает вид:
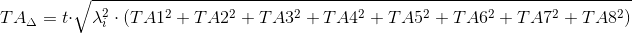
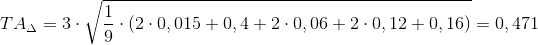
3. Координаты середины поля допуска замыкающего звена
Координату середины поля допуска замыкающего звена определим по формуле
Для заданной размерной цепи формула (5) принимает вид:
С(AΔ) = С(A1) + С(A2) + С(A3) - (С(A4) + С(A5) + С(A6) + С(A7) + С(A8))
С(AΔ) = (-0,0075) + 0,15 + (-0,0075) - ((-0,03) + (-0,06) + (-0,16) + (-0,06) + (-0,03)) = 0,475 (мм)
4. Предельные отклонения замыкающего звена
4.1. Верхнее отклонение замыкающего звена EsAΔ определим по формуле EsAΔ = 0,475 + 0,5·0,471 = 0,71(мм)
4.2. Нижнее отклонение замыкающего звена EiAΔ определим по формуле EiAΔ = 0,475 - 0,5·0,471 = 0,24(мм)
Расчет размерных цепей онлайн. Обратная задача.
Замыкающее звено: