Расчет размерных цепей

Расчет размерных цепей онлайн. Прямая задача.

Задание:
Рассчитать заданную размерную цепь (см. рис. 1) по методу полной взаимозаменяемости (max/min).
Допуски на составляющие звенья определять способом равных допусков.
Сделать проверку выполненных расчетов.

Исходные данные:

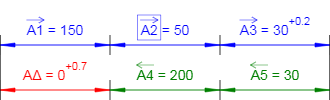
Рисунок 1 - Схема размерной цепи. Исходные данные.

Звенья размерной цепи:
A1 = 150 (мм)
A2 = 50 (мм)
A3 = 30^+0,2 (мм) - звено с известным допуском;
A4 = 200 (мм)
A5 = 30 (мм)

Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5;
Компенсирующее звено: A2
Замыкающее звено: AΔ
Верхнее отклонение замыкающего звена Es(AΔ) = 0,7 мм
Нижнее отклонение замыкающего звена: Ei(AΔ) = 0 мм

Решение:
1. Определение характеристик замыкающего звена.

1.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:

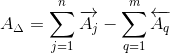(1)

где
A _j – номинальный размер любого увеличивающего звена;
A _q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;

Тогда для заданной размерной цепи формула (1) принимает вид:
AΔ = A1 + A2 + A3 - (A4 + A5)
AΔ = 150 + 50 + 30 - (200 + 30) = 0(мм)

1.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:

T(A Δ ) = Es(A Δ ) - Ei(A Δ )

(2)

где
Es(A _Δ ) – верхнее отклонение замыкающего звена;
Ei(A _Δ ) – нижнее отклонение замыкающего звена;

тогда
T(AΔ) = 0,7 - 0 = 0,7(мм)

2. Определение характеристик составляющих звеньев размерной цепи.

2.1. Определение допусков составляющих звеньев
2.1.1 Определение среднего допуска
Средний допуск определим по формуле:

(3)

где
T(A _Δ) - допуск замыкающего звена;
T(A _s ) - допуск звена с известным допуском;
k – число звеньев размерной цепи;
u - число звеньев с известным допуском;
s - индекс звена с известным допуском;

тогда

T(Aср) =	0,7 - 0,2	= 0,125 (мм)
	5 - 1

2.1.2 Определение допусков составляющих звеньев с известными отклонениями
Допуски звеньев определяем по формуле (2):
T(A3) = 0,2 - 0 = 0,2(мм);

2.2. Назначение отклонений на звенья размерной цепи
На увеличивающие звенья допуски назначаются в "+", а на уменьшающие звенья допуски назначаются в "-"
A1 = 150^+0,125 (мм);
A4 = 200_-0,125 (мм);
A5 = 30_-0,125 (мм);

2.3. Определение середины поля допуска i-го звена
Середину поля допуска i-го звена определим по формуле:

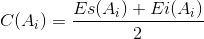(4)

где
Es(A _i ) – верхнее отклонение звена;
Ei(A _i ) – нижнее отклонение звена;

тогда

С(A1) =	(0,125 + 0)	= 0,0625
	2

С(A3) =	(0,2 + 0)	= 0,1
	2

С(A4) =	(0 + (-0,125))	= -0,0625
	2

С(A5) =	(0 + (-0,125))	= -0,0625
	2

3. Определение характеристик компенсирующего звена.

Компенсирующее звено: A2 - увеличивающее звено

3.1. Определение допуска компенсирующего звена.
Допуск компенсирующего звена определим по формуле:

(5)

где
Т(А _i ) – допуск любого составляющего звена;
T(A _k) - допуск компенсирующего звена;

Тогда для заданной размерной цепи формула (5) принимает вид:
T(A2к) = T(AΔ) - (T(A1) + T(A3) + T(A4) + T(A5))
тогда
T(A2к) = 0,7 - (0,125 + 0,2 + 0,125 + 0,125) = 0,125 (мм)

3.2. Определение середины поля допуска компенсирующего звена
Середину поля допуска компенсирующего звена определим по формуле:

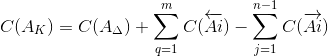(6)

где
C(A _j ) - координата середины поля допуска любого увеличивающего звена;
C(A _q ) - координата середины поля допуска любого уменьшающего звена;
C(A _Δ) - координата середины поля допуска замыкающего звена

Тогда для заданной размерной цепи формула (6) принимает вид:
C(A2к) = C(AΔ) + (C(A4) + C(A5)) - (C(A1) + C(A3))
тогда
C(A2к) = 0,35 + ((-0,0625) + (-0,0625)) - (0,0625 + 0,1) = 0,0625

3.3. Определение верхнего отклонения компенсирующего звена
Верхнее отклонение компенсирующего звена определим по формуле:

Es(Ak ) = C(Ak ) + 0,5⋅T(k )

(7)

где
C(A _k) - координата середины поля допуска компенсирующего звена;

тогда
Es(Aк) = 0,0625 + (0,5⋅0,125) = 0,125

3.4. Определение нижнего отклонения компенсирующего звена
Нижнее отклонение компенсирующего звена определим по формуле:

Ei(Ak ) = C(Ak ) - 0,5⋅T(k )

(8)

тогда
Ei(Aк) = 0,0625 - (0,5⋅0,125) = 0

Результаты расчета.

Звенья размерной цепи с определенными допусками:
A1 = 150^+0,125 (мм);
A2 = 50^+0,125 (мм);
A3 = 30^+0,2 (мм);
A4 = 200_-0,125 (мм);
A5 = 30_-0,125 (мм);

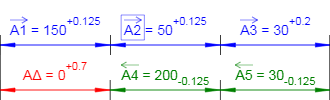
Рисунок 2 - Схема размерной цепи. Результаты расчета.

Проверка расчета.

Проверка правильности решения задачи производится по формулам:
Верхнее отклонение замыкающего звена Es(A_Δ) определим по формуле:

(9)

где
Es(A _j ) – верхнее отклонение любого увеличивающего звена;
Ei(A _q ) – нижнее отклонение любого уменьшающего звена;

Тогда для заданной размерной цепи формула (9) принимает вид:
Es(AΔ) = Es(A1) + Es(A2) + Es(A3) - (Ei(A4) + Ei(A5))
тогда
Es(AΔ) = 0,125 + 0,125 + 0,2 - ((-0,125) + (-0,125)) = 0,7

Нижнее отклонение замыкающего звена Ei(A_Δ) определим по формуле:

(10)

где
Ei(A _i ) – нижнее отклонение любого увеличивающего звена;
Es(A _q ) – верхнее отклонение любого уменьшающего звена;

Тогда для заданной размерной цепи формула (10) принимает вид:
Ei(AΔ) = Ei(A1) + Ei(A2) + Ei(A3) - (Es(A4) + Es(A5))
тогда
Ei(AΔ) = 0 + 0 + 0 - (0 + 0) = 0

Расчет размерных цепей онлайн. Прямая задача.