Расчет размерных цепей
Обратная задача
метод максимума-минимума
Метод максимума-минимума учитывает только предельные отклонения звеньев размеров цепи и самые неблагоприятные их сочетания, обеспечивает заданную точность сборки без подгонки деталей, то есть полную взаимозаменяемость.
Расчет размерных цепей онлайн. Обратная задача.
Формулы
1. Определение характеристик составляющих звеньев размерной цепи
1.1. Допуск составляющего звена определяется по формуле:
1.2. Середину поля допуска i-го звена определим по формуле:
2. Определение характеристик замыкающего звена
2.1.
Номинальный размер замыкающего звена определяется по формуле:
2.2. Допуск замыкающего звена определяется по формуле:
2.3.
Координата середины поля допуска замыкающего звена определяется по формуле:
2.4. Предельные отклонения замыкающего звена.
2.4.1 Верхнее отклонение замыкающего звена Es(AΔ) определяется по формуле:
2.4.2. Нижнее отклонение замыкающего звена Ei(AΔ) определяется по формуле:
Пример
Задание:
Требуется проверить наличие и величину зазора AΔ.
Рассчитать заданную размерную цепь (см. рис. 1) по методу максимума-минимума.
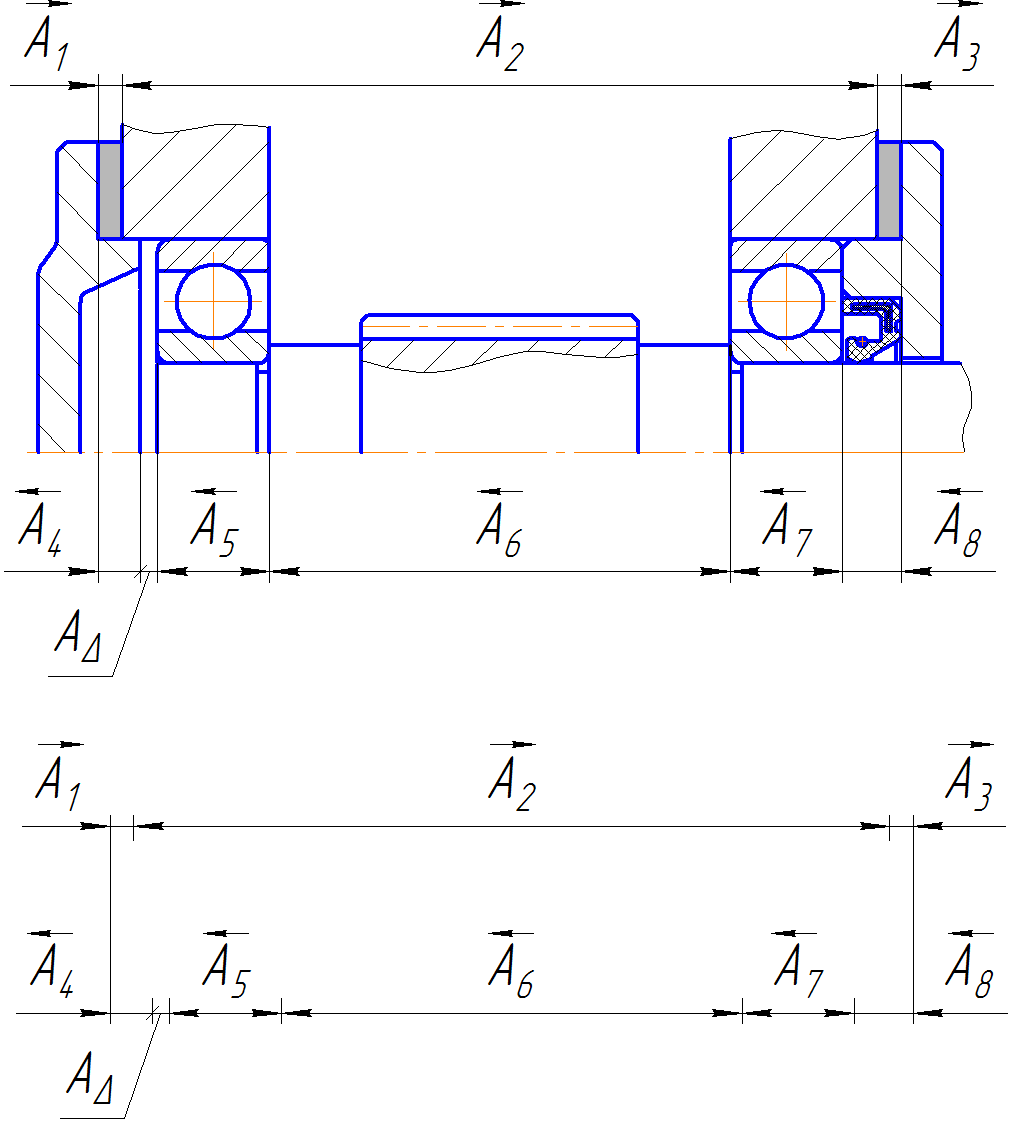
Рисунок 1 – Сборочная размерная цепь.
Исходные данные:
Звенья размерной цепи:
Допуски и координаты середины поля допуска составляющих звеньев определены по формулам (1) и (2)
Увеличивающие звенья: A1 , A2 , A3;
Уменьшающие звенья: A4, A5, A6, A7, A8;
Замыкающее звено: AΔ
Решение:
1. Номинальный размер замыкающего звена
Номинальный размер замыкающего звена AΔ определим по формуле (3)
Для заданной размерной цепи формула (3) принимает вид:
AΔ = A1 + A2 + A3 - (A4 + A5 + A6 + A7 + A8)
AΔ = 1 + 206 + 1 - (10 + 19 + 150 + 19 + 10) = 0(мм)
2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле (4)
Для заданной размерной цепи формула (4) принимает вид:
T(AΔ) = T(A1) + T(A2) + T(A3) + T(A4) + T(A5) + T(A6) + T(A7) + T(A8)
TAΔ = 0,015 + 0,4 + 0,015 + 0,06 + 0,12 + 0,16 + 0,12 + 0,06 = 0,95(мм)
3. Координаты середины поля допуска замыкающего звена
Координату середины поля допуска замыкающего звена определим по формуле (5)
Для заданной размерной цепи формула (5) принимает вид:
С(A Δ) = С(A1) + С(A2) + С(A3) - (С(A4) + С(A5) + С(A6) + С(A7) + С(A8))
С(AΔ) = (-0,0075) + 0,15 + (-0,0075) - ((-0,03) + (-0,06) + (-0,16) + (-0,06) + (-0,03)) = 0,475 (мм)
4. Предельные отклонения замыкающего звена
4.1. Верхнее отклонение замыкающего звена EsAΔ определим по формуле (6)
EsAΔ = 0,475 + 0,5·0,95 = 0,95(мм)
4.2. Нижнее отклонение замыкающего звена EiAΔ определим по формуле (7)
EiAΔ = 0,475 - 0,5·0,95 = 0(мм)
Замыкающее звено A ∆ = 0 +0,95 (мм); T(AΔ)=0,95 (мм)
1. Определение характеристик составляющих звеньев размерной цепи
1.1. Допуск составляющего звена определяется по формуле:
| T(A i ) = Es(A i ) - Ei(A i ) | (1) |
где
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
i – индекс звена;
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
i – индекс звена;
1.2. Середину поля допуска i-го звена определим по формуле:
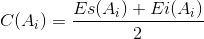 | (2) |
2. Определение характеристик замыкающего звена
2.1.
Номинальный размер замыкающего звена определяется по формуле:
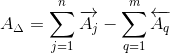 | (3) |
где
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
2.2. Допуск замыкающего звена определяется по формуле:
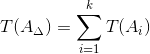 | (4) |
где
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
2.3.
Координата середины поля допуска замыкающего звена определяется по формуле:
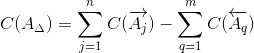 | (5) |
где
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
C(A j ) - координата середины поля допуска любого увеличивающего звена;
C(A q ) - координата середины поля допуска любого уменьшающего звена;
2.4. Предельные отклонения замыкающего звена.
2.4.1 Верхнее отклонение замыкающего звена Es(AΔ) определяется по формуле:
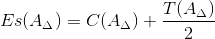 | (6) |
где
C(A Δ) - координата середины поля допуска замыкающего звена
T(A Δ) - допуск замыкающего звена;
C(A Δ) - координата середины поля допуска замыкающего звена
T(A Δ) - допуск замыкающего звена;
2.4.2. Нижнее отклонение замыкающего звена Ei(AΔ) определяется по формуле:
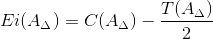 | (7) |
Пример
Задание:
Требуется проверить наличие и величину зазора AΔ.
Рассчитать заданную размерную цепь (см. рис. 1) по методу максимума-минимума.

Рисунок 1 – Сборочная размерная цепь.
Исходные данные:
Звенья размерной цепи:
Допуски и координаты середины поля допуска составляющих звеньев определены по формулам (1) и (2)
| A1 = 1-0,015 (мм); | Т(A1)=0,015 (мм); | C(A1) = -0,0075 (мм); | ||||
|
Т(A2)=0,4 (мм); | C(A2) = 0,15(мм); | ||||
| A3 = 1-0,015 (мм); | Т(A3)=0,015 (мм); | C(A3) = -0,0075 (мм); | ||||
| A4 = 10-0,06 (мм); | Т(A4)=0,06 (мм); | C(A4) = -0,03 (мм); | ||||
| A5 = 19-0,12 (мм); | Т(A5)=0,12 (мм); | C(A5) = -0,06 (мм); | ||||
|
Т(A6)=0,16 (мм); | C(A6) = -0,16 (мм); | ||||
| A7 = 19-0,12 (мм); | Т(A7)=0,12 (мм); | C(A7)= -0,06 (мм); | ||||
| A8 = 10-0,06 (мм); | Т(A8)=0,06 (мм); | C(A8)= -0,03 (мм); |
Увеличивающие звенья: A1 , A2 , A3;
Уменьшающие звенья: A4, A5, A6, A7, A8;
Замыкающее звено: AΔ
Решение:
1. Номинальный размер замыкающего звена
Номинальный размер замыкающего звена AΔ определим по формуле (3)
Для заданной размерной цепи формула (3) принимает вид:
AΔ = A1 + A2 + A3 - (A4 + A5 + A6 + A7 + A8)
AΔ = 1 + 206 + 1 - (10 + 19 + 150 + 19 + 10) = 0(мм)
2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле (4)
Для заданной размерной цепи формула (4) принимает вид:
T(AΔ) = T(A1) + T(A2) + T(A3) + T(A4) + T(A5) + T(A6) + T(A7) + T(A8)
TAΔ = 0,015 + 0,4 + 0,015 + 0,06 + 0,12 + 0,16 + 0,12 + 0,06 = 0,95(мм)
3. Координаты середины поля допуска замыкающего звена
Координату середины поля допуска замыкающего звена определим по формуле (5)
Для заданной размерной цепи формула (5) принимает вид:
С(A Δ) = С(A1) + С(A2) + С(A3) - (С(A4) + С(A5) + С(A6) + С(A7) + С(A8))
С(AΔ) = (-0,0075) + 0,15 + (-0,0075) - ((-0,03) + (-0,06) + (-0,16) + (-0,06) + (-0,03)) = 0,475 (мм)
4. Предельные отклонения замыкающего звена
4.1. Верхнее отклонение замыкающего звена EsAΔ определим по формуле (6)
EsAΔ = 0,475 + 0,5·0,95 = 0,95(мм)
4.2. Нижнее отклонение замыкающего звена EiAΔ определим по формуле (7)
EiAΔ = 0,475 - 0,5·0,95 = 0(мм)
Замыкающее звено A ∆ = 0 +0,95 (мм); T(AΔ)=0,95 (мм)